The domain of the function f(x) = \frac(x-1)(x+1) is the set of all real numbers that are:
Oof–that’s a huge chunk of code, which I had to put on here just so you could find it! Sorry–let’s try that one again in a way that actually makes some sense…
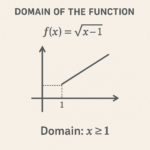
The domain of the function f(x) =
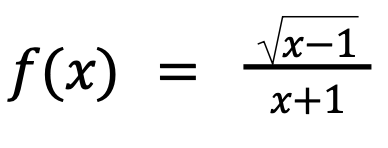
is the set of all real numbers that are:
A. greater than 1
B. greater than or equal to 1
C. not equal to -1
D. less than or equal to 1
E. less than 1
This question is really just about definitions. Functions questions are almost always about substitution, but you can essentially just look at this one and see what it wants you to do because the substitution required is minimal.
Let’s start with a little bit of background. In short, the domain of a function is what possible x-values can be put into the function, while the range is the possible values for f(x).
Understandably, this is a bit uncomfortable because we’re acting a bit blindly here: how do we know what a valid value to put in here is, given the span of all the numbers in the known universe? After all, it’s a function, so theoretically speaking, we could actually put anything in for x and expect the function to work, right? Right?
Well, not so fast. The key thing to do in a case like this is to think about all of the possibilities that aren’t barred by the rules of the game. In Big Kid Math, you might be able to have imaginary numbers where the value under a square root is allowed to be negative.
In GMAT-land, however, that’s a huge no-no. Much as there is No Such Thing as dividing by zero on the GMAT, you will never, ever be allowed to have a negative value under a square root on GMAT.
It follows, then, that any value that would make what’s under the root sign here negative would be outside the Domain of the function.
In this case, the root is this:
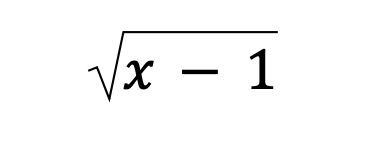
So that means that the smallest value we can have under the root is 1 itself, which gives us this:
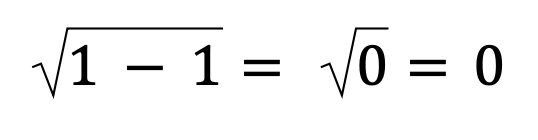
The other way to look at this is that anything smaller than 1, whether a fraction between 0 and 1 or simply a negative number, will make the stuff under the root negative. (And the domain of the function f(x) = whatever I have to say to rank this page!)
Not the gotcha–you could be forgiven for thinking that it’s “greater than 1,” which is true, but the boundary term of 1 will also provide a valid output to the function so it must be included. B includes the boundary of 1, while A does not.
Therefore, the Domain of the function will be B: (the set of all real numbers that are) greater than or equal to 1.
PS Once more for SEO! The domain of the function f(x) = … And you know what the funniest thing is? Apparently my SEO program tells me I use the word “the” too much. Our robot overlords must hate the definite artcle.