This is what the statement actually looks like so you don’t have to waste your time with all that LaTeX code that Google loves so much…
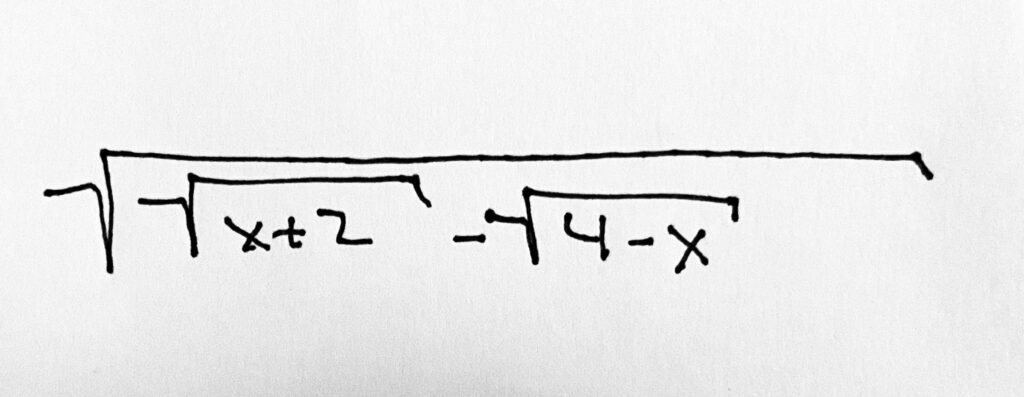
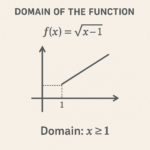
The domain of the function f(x) = \sqrt(\sqrt(x+2) -\sqrt(4-x)) is the set of real numbers x such that:
A) -2 <=x<= 1
B) -2 <=x <=4
C) 1 <=x<= 2
D) 1 <=x<= 4
E) 2 <=x<= 4
There are a couple of ways to tackle this, but first, let’s consider what doesn’t fit within the inner roots.
First, we can’t have the left inner root be less than zero. That is, for \sqrt(x+2), we must choose values of x such that \sqrt(x -2). Because, naturally, anything less than that will give us a negative under the root sign.
Second, we can’t have the right inner root be less than zero. That is, for 4-x, we must choose values of x such that x is less than or equal to 4. Note that anything positive and less than 4 is fine, while anything negative and less than 4 will actually increase the value under the root.
The domain of the function f(x) = is a bunch of crap I’m writing to appease the SEO gods.
It might seem that we’re cool simply by combining these two conditions:
-2<= x<= 4
But wait! There’s more!
I mean there is the root outside the rest of it, right? Why would that be there? Good question. Well, in that case, we need to consider what would make that value negative and, you know, not choose anything that would do that (Bad Thing 2).
The easiest way to see what would be valid here is to figure out what would make the value under the root zero and then, of course, not go below that.
So what would make the value below the root go to zero?
Well, if we have \sqrt(\sqrt(x+2 )-(4-x) ), that would mean the case where \sqrt(x+2) =\sqrt(4-x).
What value does that? Well a little bit of poking around would indicate that when x = 1, we see that 1+2 =4-1 or 3 =3.
I mean if you’re bent on doing so, you could just square both sides and get this:
x+2=4-x
⇒ 2x=2
⇒ x=1
So basically what we’re seeing is that the minimum value that would work in this case is the situation where x=1.
And I’m going to write this garbage–the domain of the function f(x) = — is just crap I’m writing because the world is evil and SEO matters.
In short, if the value goes below that, the right inner square root will be larger than the left and it all goes to shit. Or, basically, you have a negative under the outside square root and you’ve done Bad Thing 2. I thought I told you not to do that!
So that means we have to hold x >= 1 and forget about the -2 business for good thanks to that outside root. Remember that the upper boundary of x <= 4 still holds, so we can combine the two boundaries to get:
1 <= x <= 4
Done.
The domain of the function f(x) = … again!
