Chapter 11: GMAT Triangles
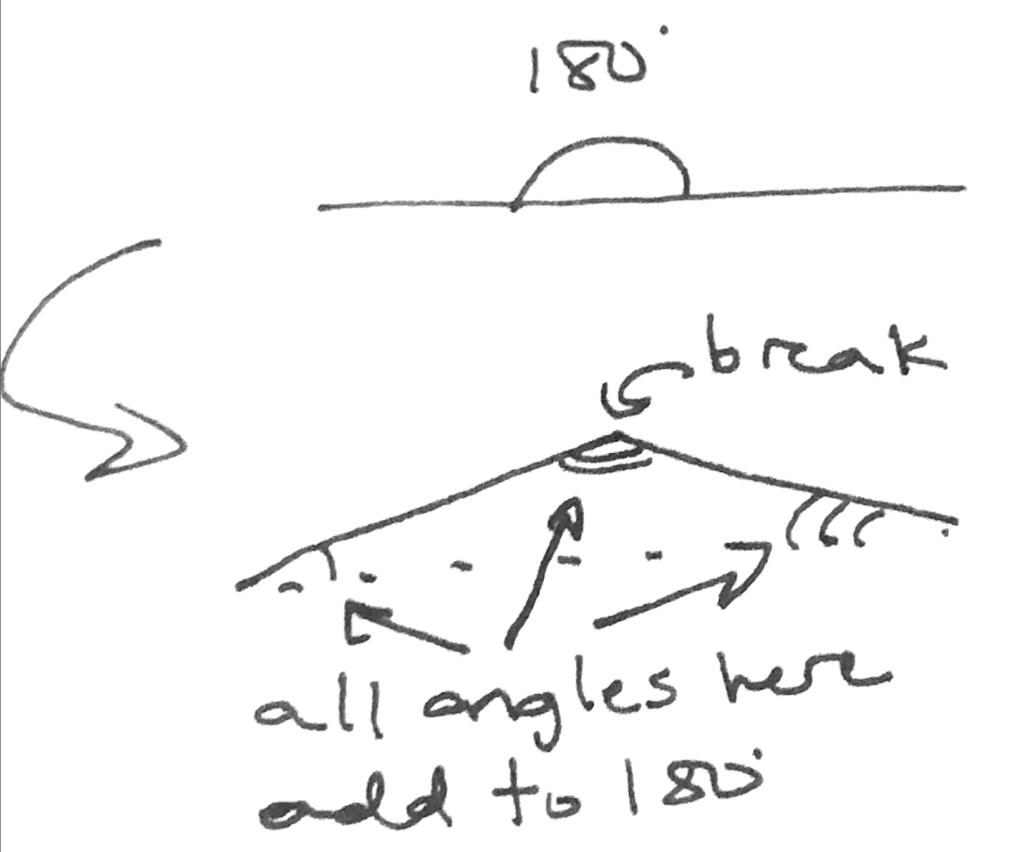
All the basic stuff for triangles is probably going to be fairly obvious. First, of course, a triangle is a three-sided object. Second is that all of the angles of a triangle add to 180 degrees.
Third is that the angle opposite any side of the triangle is proportional to that side. Bearing that in mind, we can set up correspondences such as these:
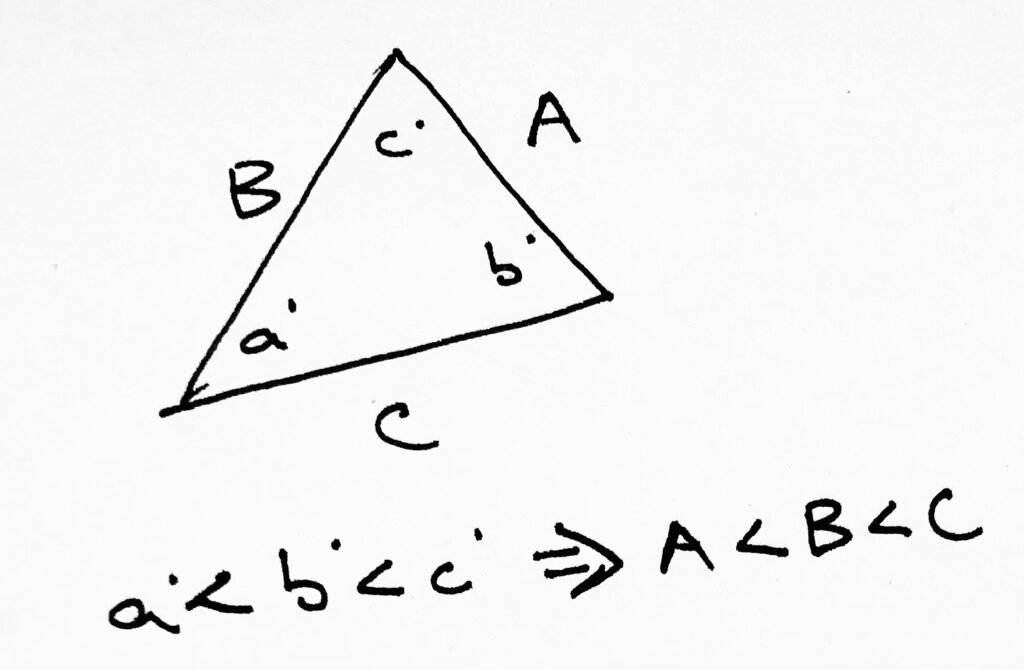
It is, again, probably painfully obvious, but remember that the smallest side will of course correspond to the smallest angle, the middle side will correspond to the middle angle, and the largest side will correspond to the largest angle.
Another interesting point we can make is that if we define the “outside angles” of a triangle as the angles created by continuation of each line outward, like this…
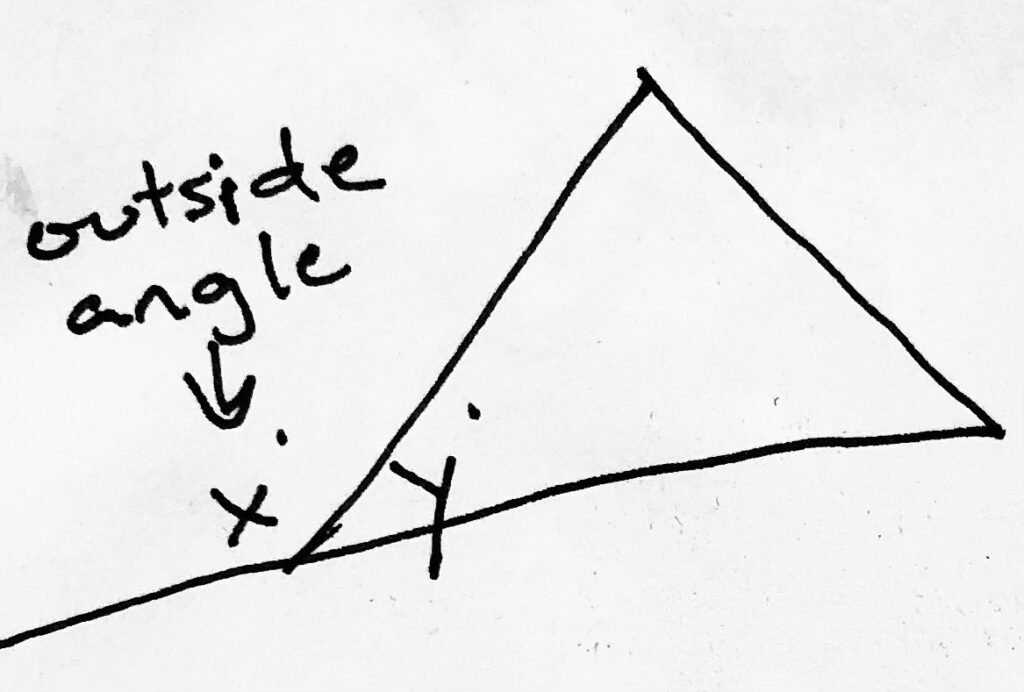
…then we can say that the sum of these exterior angles will yield 360 degrees. Like this:
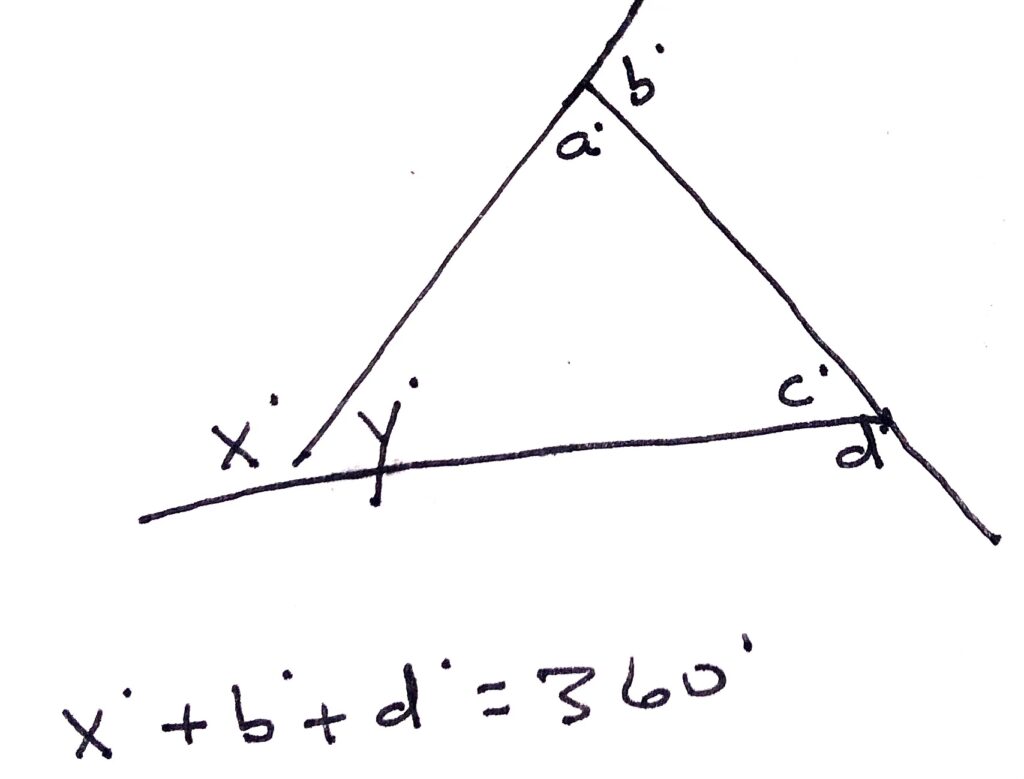
Another way to think about this would be that it’s the sum of the supplements of each of the interior angles.
The perimeter of a triangle is probably fairly easy to figure out: just add the lengths of the three sides.
The area of a triangle might be more tricky, but it’s worth looking at where it comes from. First, let’s just come out with the whole formula:

So if it’s 1/2bh, then what’s up with the ½ part? Look at it this way. For any triangle, you can simply double it and create a parallelogram. Like this:
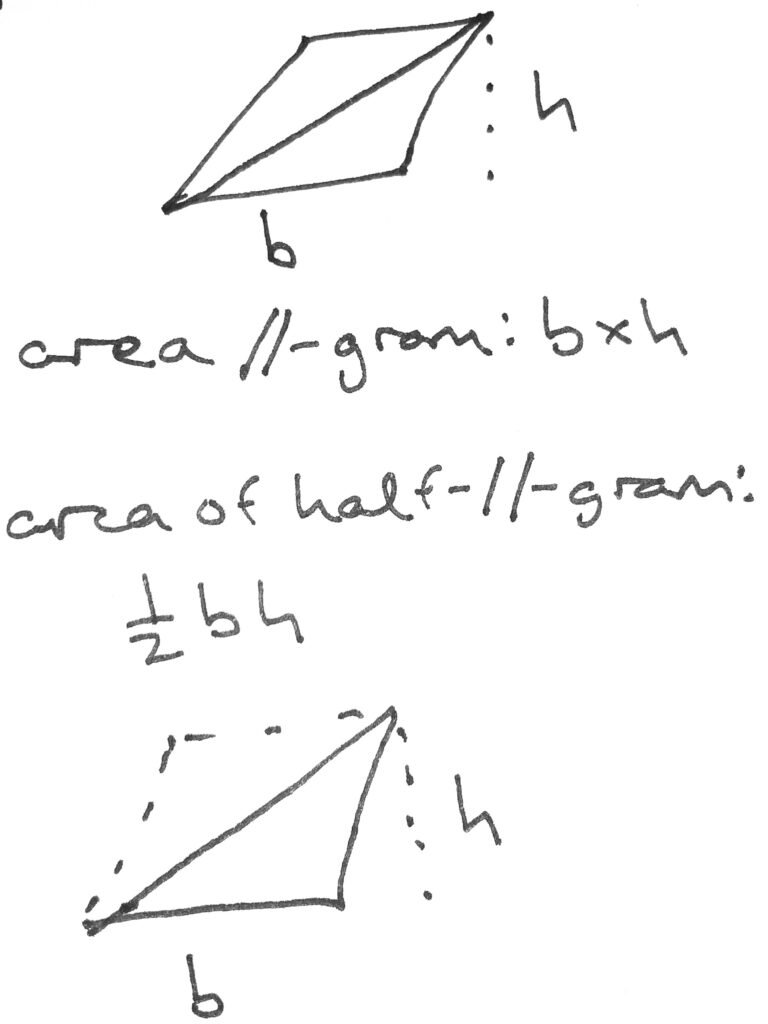
Remember that the area of any parallelogram is just base times height or bh. So if any parallelogram can be halved like this to make a triangle, it follows that the area of the triangle made by halving the parallelogram would have an area of 1/2bh.
Chapter 12: Triangle Inequality Theorem for GMAT Triangles
This concept is really easy to see but really difficult to explain with words. In short, if you’re given two sides of a triangle but don’t know the third side, certain side lengths for the third side simply won’t work.
Like this:
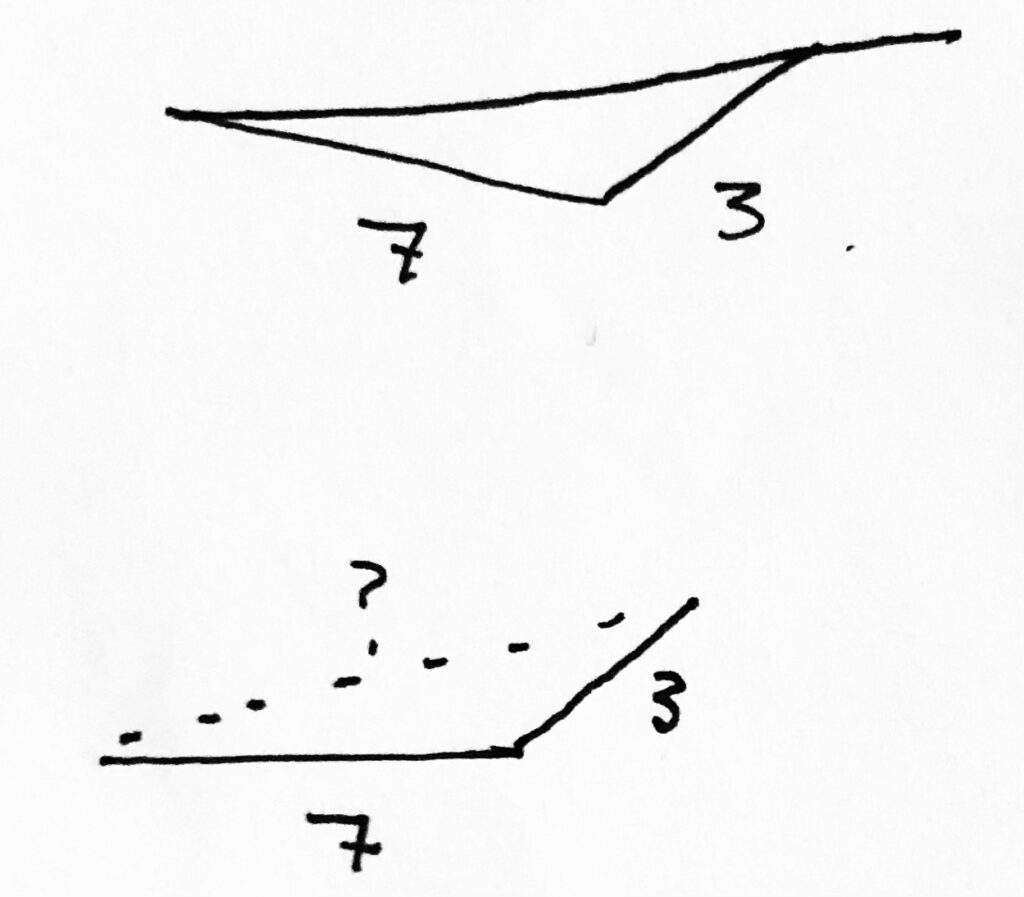
Some of them will be too long, like this:
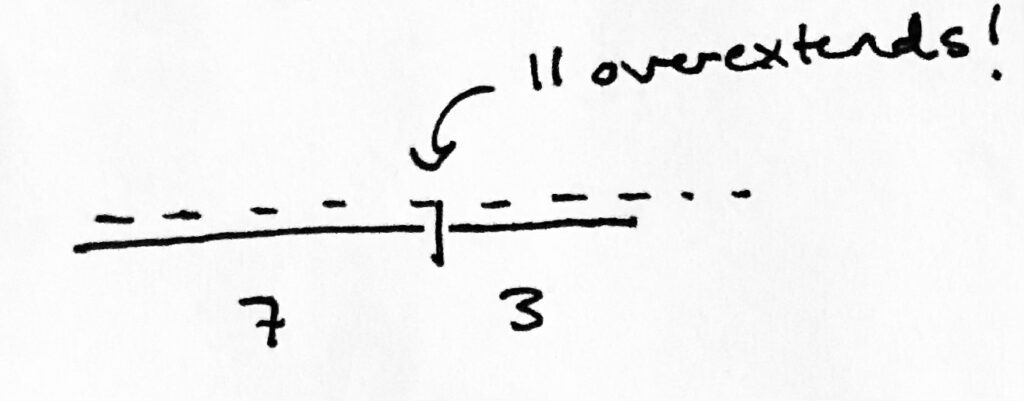
Some of them will be too short, like this:
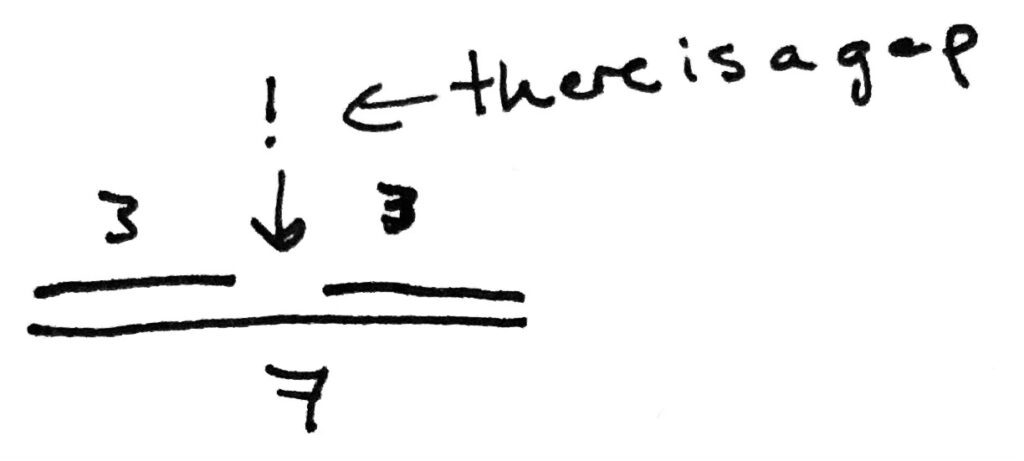
The question, then, is how we tell what the possible lengths that we might use are. The way to do this is to imagine the two sides that we know as effectively having hinges so that we can extend them fully or, alternatively, close one in over the other. Like this:
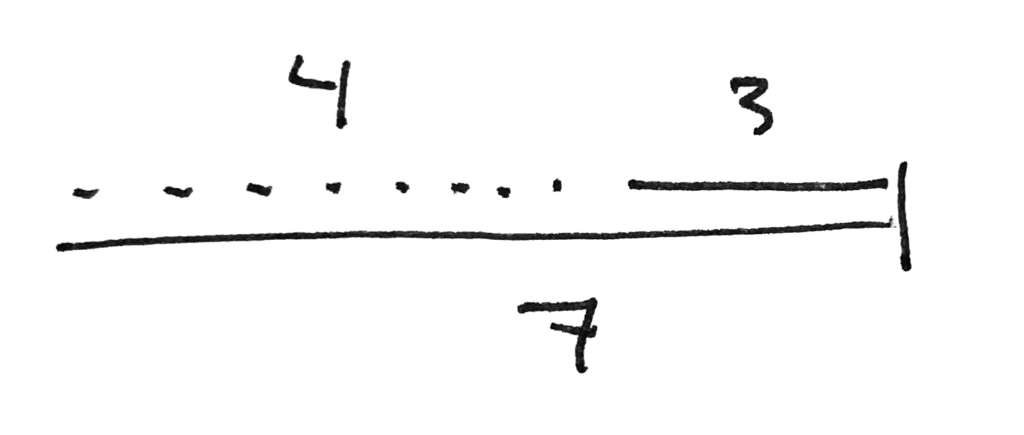
On one hand, we effectively create a triangle with a 0-degree angle (which, obviously, isn’t actually a triangle but play along here for the sake of argument). On the other, we effectively create a triangle with a 180-degree angle (same goes).
In essence, that tells us that the unknown side must have a length somewhere between the sum and the difference of the other two angles.
So, for example, if we know that our triangle has a side of 7 and a side of 4, we can say that the potential lengths of the third side would be within this range:
7-4<x<7+4
3<x<11
The key to this is to remember to apply it in circumstances where we’re not given much information (Data Sufficiency, anyone?). If you can’t absolutely establish the value of the third side, it is vital that you run it through the Triangle Inequality Theorem to make sure that the third side is even a damn possibility.
Chapter 13: Isosceles Triangles — GMAT Triangles
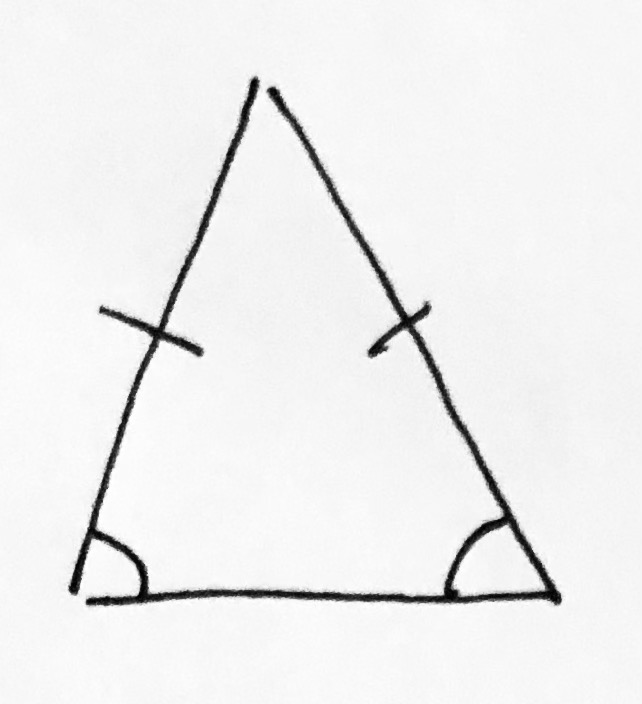
An isosceles triangle is a triangle that has two equal sides. This is easy enough to remember if you recall that the Greek root iso means “equal” and that the Greek root cel means “side.”
It follows from what we’ve learned so far that if the triangle has two equal sides, it must also have two equal angles.

What these angles are doesn’t really matter except that they must, of course, add with the third side to make 180 degrees.
A special case is the Right Isosceles or 45:45:90 triangle, which we will address in a later section.
Chapter 14: Equilateral Triangles
Equilateral triangles have three equal sides, and, of course, three equal angles to correspond to these three equal sides.
Math likes to mix it up with the Greek versus Latin by using the Latin equi to mean “equal” and lat to mean “side.” Maybe there’s something to the Greek “equal-sided” implying two sides the same and the Latin “equal-sided” implying three sides the same. Probably not.
Anyhow, equilateral triangles are like any other triangle insofar as the sum of their angles must be 180 degrees. We know from above that all of the three angles must be equal, which therefore implies that the value of each of the angles must be 180/3=60 degrees.
Like this:
One thing to note at this point is that if you split an equilateral triangle in two, you arrive at a 30:60:90 triangle, which is actually necessary to prove the area of an equilateral triangle.
We’ll get into that in the Special Triangles in GMAT Triangles section.
Chapter 15: Right Triangles — GMAT Triangles
At this point, we’ve discussed what a right angle is, but we have barely touched upon its implications in the world of triangles.
A right triangle is, unsurprisingly, a triangle that has one right angle. Why only one? Well, if a triangle’s interior angles must sum to 180 degrees and a right angle is 90 degrees, it would be pretty hard to have more than one. Try to draw it; you’ll see what I’m talking about.
Here are some useful definitions:
—legs are the sides of the triangle adjacent to the right angle
–the hypotenuse is the side of the triangle opposite the right angle
Like this:
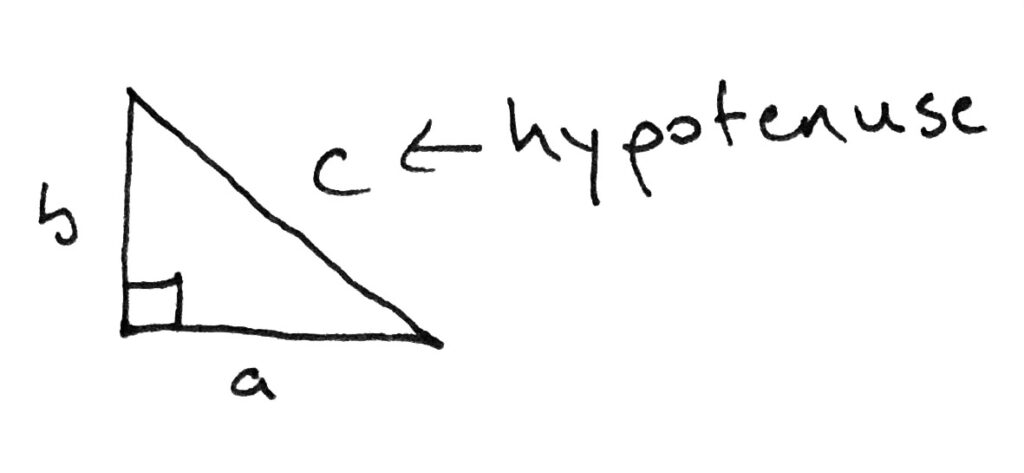
By far the most useful thing about right triangles is that they mysteriously obey what is called the Pythagorean Theorem, which states, qualitatively, that the sum of the squares of the legs of the triangle is equal to the square of the hypotenuse. No shit–for realz!
Like this:
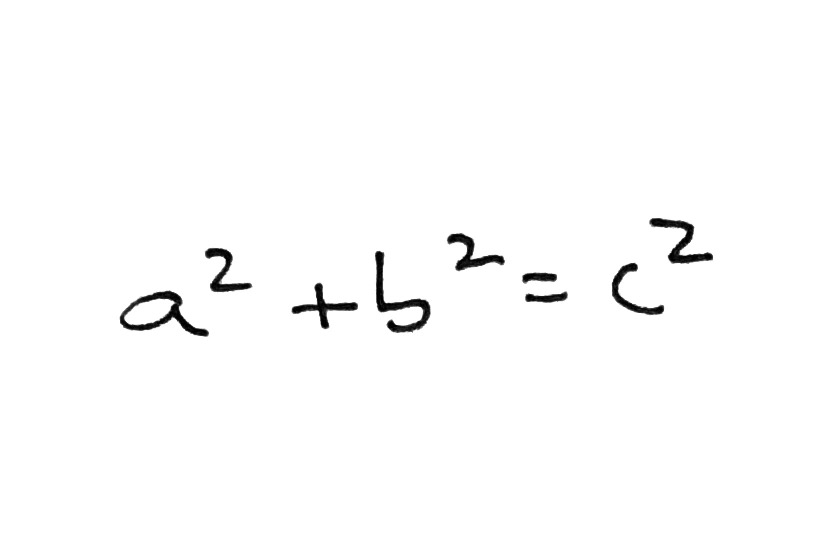
Now, the difficult thing about this is proving it. It’s honestly one of those things that’s better just accepted because it works, and that’s all you need for GMAT triangles.
That’s not to suggest you not try! After all, Pythagoras lived in a cave, was widely regarded as a crackpot, and had a renowned commitment to “mystery rites,” or as moderns prefer, tripping balls. To paraphrase Hunter Thompson, “I hate to advocate insanity or the Eleusinian Mysteries to anyone, but they seem to have worked for Pythagoras.” We’re still talking about old Pythagoras, though, eh?
Just do all that after the GMAT, please.
Also–has anyone ever noticed how in the UK people say “I can just apply Pythagoras here…” like it’s something you find in a jar next to the Marmite? Yeah, I don’t get it either.
PS Does the Pythagorean Theorem work for non-right triangles? Short answer: not as far as we’re concerned. All GMAT triangles are either right or non-right; there’s no middle ground.
Chapter 16: Similar vs. Congruent (You Can Probably Ignore This for GMAT Triangles)
If two triangles are similar, that means they share the same angles. Further to this, the sides opposite these angles will be in a specific ratio to one another.
This might be better established with an example. Let’s say that we have two similar triangles, each of which are 45:45:90 triangles (we’ll be seeing a lot of these later). That is, they have the same angles.
If the hypotenuse of one of these triangles is sqrt2, and the hypotenuse of the other triangle is 3sqrt2, then we know that the other two legs will also be a factor of 3 larger than the legs of the sqrt2 triangle.

On the other hand, congruent triangles still have all the same angles, but they also have the same side lengths corresponding to those angles. In other words, they are the same.
Or maybe not the same, which would be sort of like saying that identical twins are the same person. Maybe a better way to put it is that two congruent triangles are identical copies of one another.
Remember, though, you don’t need to know this terminology for GMAT triangles, although understanding that similar triangles share angles can definitely be helpful in some trickier questions.
Chapter 17: GMAT Triangles Examples Thus Far
One of the largest mistakes that one could make with regard to triangles is to assume that every triangle is one of the Special Triangles that we’ll discuss in the next section.
While it is true that the majority of GMAT triangles questions do involve one of the four Special Triangles, there is no reason to torture a triangle into fitting if it clearly doesn’t fit.
Now that we’ve looked at how the non-Special Triangle triangles appear on the GMAT, let’s dig into the more common stuff: the actual Special Triangles.