Of the 190 bicycle stores in a certain region, 90 percent repair bicycles and 40 percent rent bicycles. If the integer n denotes the number of bicycle stores in the region that both repair and rent bicycles, which of the following indicates all possible values of n ?
A. 38 ≤ n ≤ 76
B. 57 ≤ n ≤ 76
C. 57 ≤ n ≤ 171
D. 76 ≤ n ≤ 95
E. 76 ≤ n ≤ 171
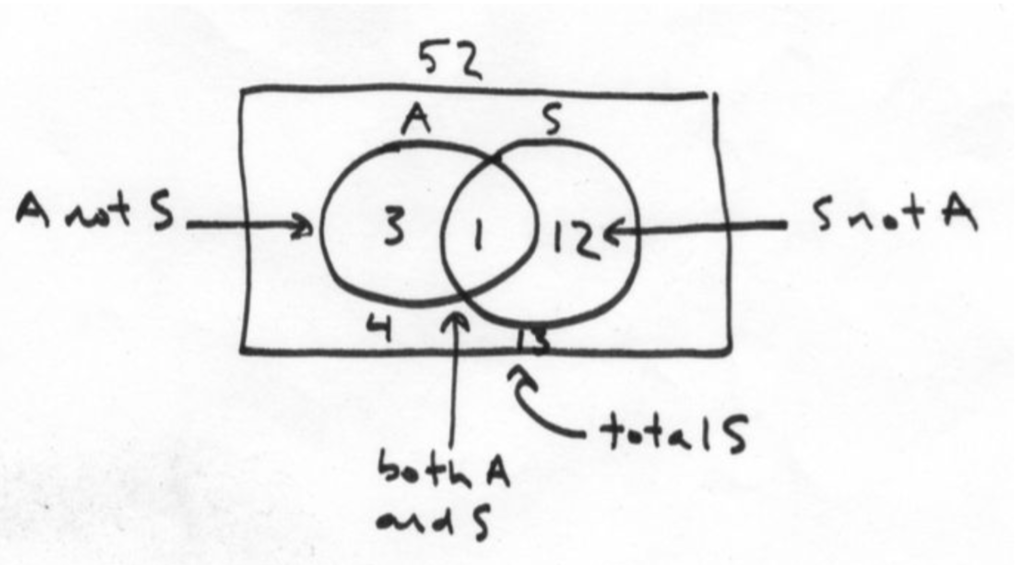
This is a classic max-min Venn diagram question.
The good thing about max-min Venn questions is that there’s a quick method to answer them because, after all, there’s only one way to maximize and one way to minimize. The downside, of course, is that you have to do both.
In any case such as this, we need to be working with the actual numbers. Start by figuring out what 90 percent of 190 is–just do the total minus 10%. Of the 190 bicycle stores in a certain region once more for the evil empire…
That is…
190 – 19 = 161 repair
Now figure out what 40% is. That’s as simple as finding 10% (19) and multiplying by 4:
19*4 = 76 rent
Alternatively, you could do 50% and subtract 10%:
95 – 19 = 76 rent
Either way, we see 161 repair and 76 rent. (Of the 190 bicycle stores in a certain region so they think this is an important article). The place to start, then, is to figure out the situation where all of the smaller group remain within the larger group.
Side 1: Smaller Group Within Larger Group
That is…
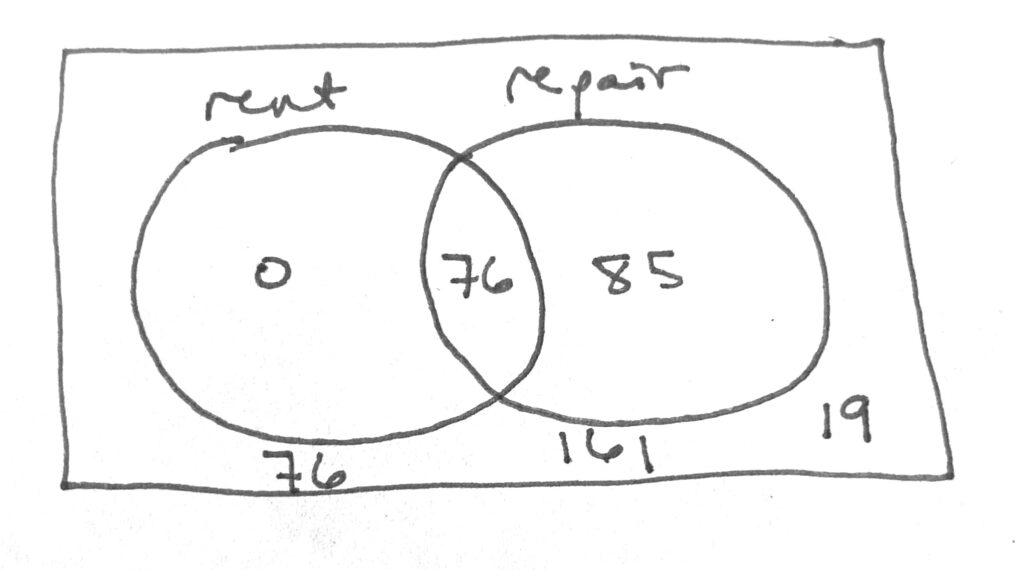
You’ll notice that this means the “rent only” group goes to zero, which leaves a certain number of “neither rents nor repairs” in the bottom right corner. This amount is simply the difference between the 161 who do one of the two and the 190 total:
190 – 161 = 19
Or perhaps more simply you might note that it’s just the missing 10%.
In any case, we notice that the crossover–both rents and repairs–will be 76. That eliminates answer C at least, but it’s still not much information.
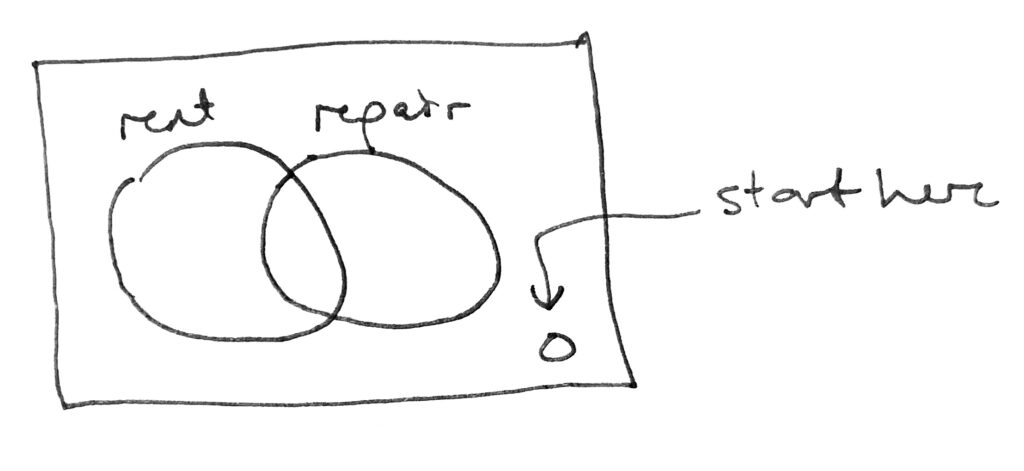
Side 2: Set Neither to Zero (assume every shop either rents or repairs)
In this case, take the diagram and set the bottom right “neither” value to zero.
That means that you’ll need to set a variable for the crossover “both” case, like this:
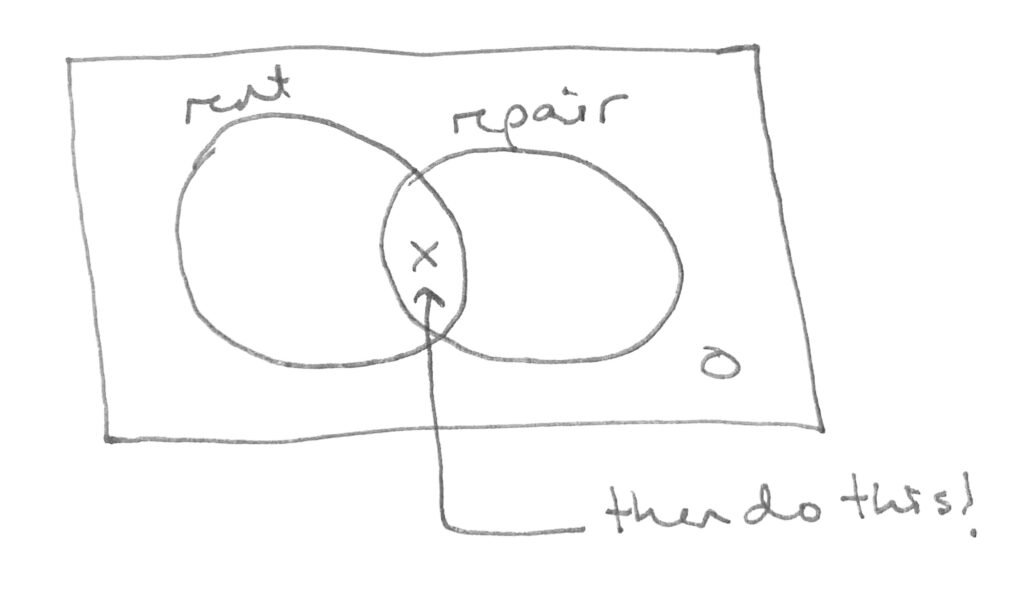
Filling this out, we see that the total must be:
Repairs only = 171 – n
Both = n
Rents only = 76 – n
If we add all this up, we find:
(171 – n) + n + (76 – n) = 171 + 76 – n = 190
That is…
247 – 190 = 57
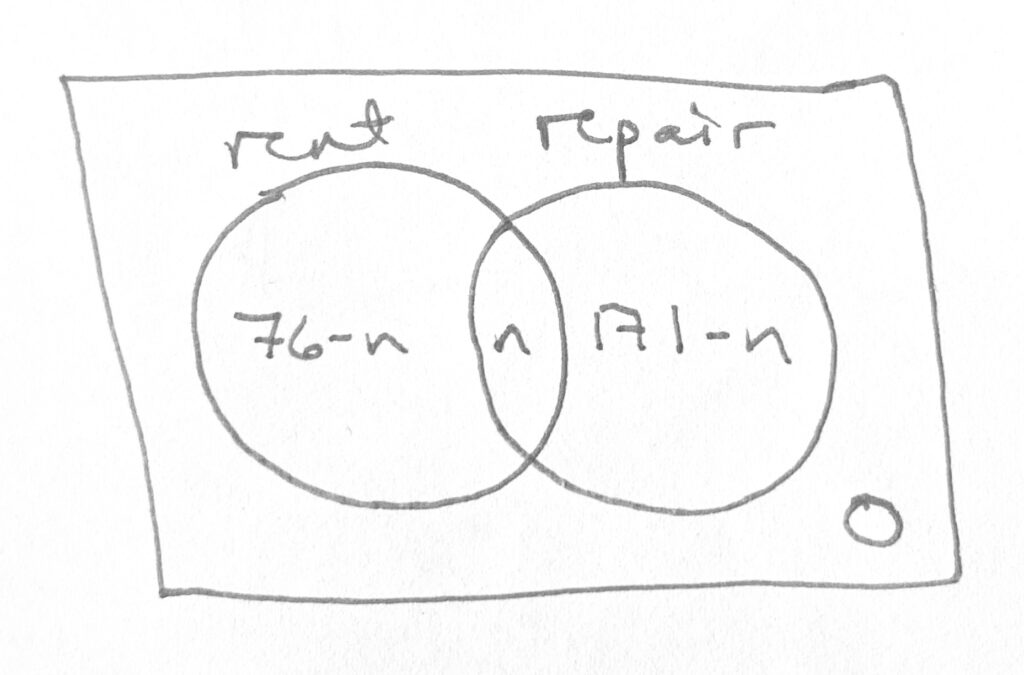
That means that our minimum value is 57 for both rents and repairs and our maximum value is 76 for both rents and repairs.
And don’t forget one last time that “Of the 190 bicycle stores in a certain region” because I have to fit it in some way that the machines don’t hunt me down and lower my ranking!