The Basic GMAT Probability Equations
First, we need to establish some sort of general definition for the term Probability itself. You’ll most often hear Probability defined as some variant of:
desired outcomes / total outcomes
First things first: Probability is always a fraction, which, of course, could also be a percent (because these two statements, at the end of the day, mean the same thing).
Second: if all of the all the desired outcomes are represented by all the total outcomes, then you have a fraction equal to 1 (or 100%).
Let’s say you want a black kitten and your neighbor’s cat just had a litter, then the Probability of getting a black kitten is the number of black kittens divided by the number of total kittens in the litter.
If we go to visit and all four kittens in the litter are black, then your Probability of getting a black kitten is:
4/4 = 1
In other words, you will invariably select a black kitten because all of the kittens are black.
That said, saying you have a 100% chance of anything is a trivial statement simply because (in most cases) this will be obvious.
In other words, the statement contains no useful information. I mean if all the cats are black, then whichever you select will be black, yes?
Probability works better, of course, when your desired outcomes are fewer than your total outcomes.
Now let’s look at the GMAT Probability equations that you’re most likely to see.
If you’re interested in more GMAT Probability resources, click here!
Basic GMAT Probability Equations
This is better learned through example.
Let’s start by imagining a normal deck of cards. That of course means 52 cards: four suits and 13 cards per suit. No jokers.
Now–for those of you who aren’t Mötörhead fans–what is the probability that, selecting one card at random from this deck, you pull the Ace of Spades?
Well, consider how many cards there are: 52. In other words, find the total outcomes, which will generally be fairly straightforward.
It makes a nice first step–nice to know that at least we’ve accomplished one thing so far!
Now we need to consider the number of desired outcomes: in this case, it’s the Ace of Spades, of which there is only one.
That is, we find that the Probability of pulling the Ace of Spades is:
1/52
Hopefully this is straightforward so far, because we need to build off the fact that it’s self-evident that we find only one Ace of Spades within the deck.
Following the same thinking, we should find four Aces in total. That means that the probability of pulling an Ace (of any suit) is:
P(A)= 4/52 = 1/13
Likewise, pulling a Spade (of any face or number) is:
P(S) = 13/52 = 1/4
Here’s the clever part: notice that 1 × 1 = 1 . In other words–using ⋀to mean “and”–we can say that:
1/13 * 1/4 = 1/52
P(A) × P(S) = P(A⋀S)
In other words, notice that when we meet the condition of “Ace” and the condition of “Spade” both, the probability actually decreases. That is, there are fewer things that are “both” than there are that are simply “one or the other.”
Another way to think about it would be to express it as a Venn diagram:
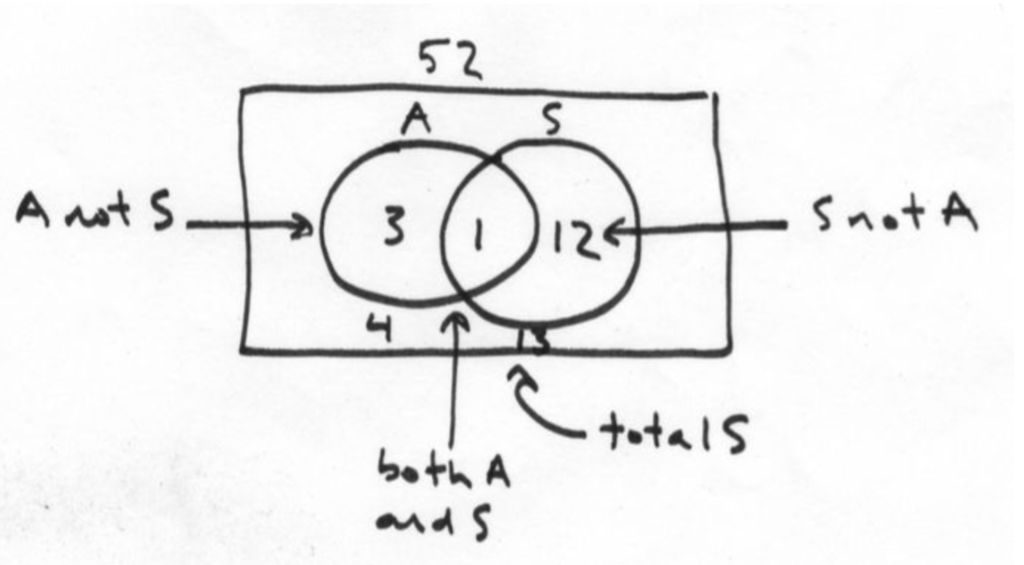
The point here is that given the fact that Probabilities are fractions less than or equal to 1, multiplying them will actually decrease the outcome.
More precisely, the Probability that two conditions must both occur is defined as the product of the Probabilities of each event.
Still with me?
In other words, if they both gotta happen, just multiply already.
The GMAT loves to test whether you multiply or add, which brings us to the next of our GMAT Probability equations.
Those times when you add
Think about it this way: we have a lot more options if you’re thinking about the Probability that you pull an Ace OR you pull a Spade.
The Probability is actually going to be, for most intents and purposes, just adding the Probability of pulling an Ace to the Probability of pulling a spade.
Why the qualification?
That has to do with this little problem: we lay out the deck of cards, it looks like the following:

It would stand to reason, of course, that if we have four Aces and 13 Spades, then the OR case would the 4 + 13 = 17 desired cards out of the total of 52.
Yet in the image… count them… count them… we see 16. Why? Notice the crossover. That card that’s in both the column and the row is–you guessed it–the Ace of Spades.
That pesky little card is actually a member of both sets, so we need to address this fact somehow.
The solution is almost annoyingly simple: we compensate for the fact that we have that extra card by finding the total value–the one that includes counting the Ace of Spades twice–and then simply subtract one of them.
Really? Is it that boneheaded?
I’m afraid so.
You’d think, after many centuries of modern Probability, that we’d be able to use some sort of clever equation to step around this problem rather than just saying “Gee, let’s simply make the mistake and then correct ourselves and we’ll totally remember to do that every single time in the future!”
Yeah, well, we haven’t got there yet. In short, you simply need to remember that crossover. Go back to the diagram; it’s the “both A and S” part:
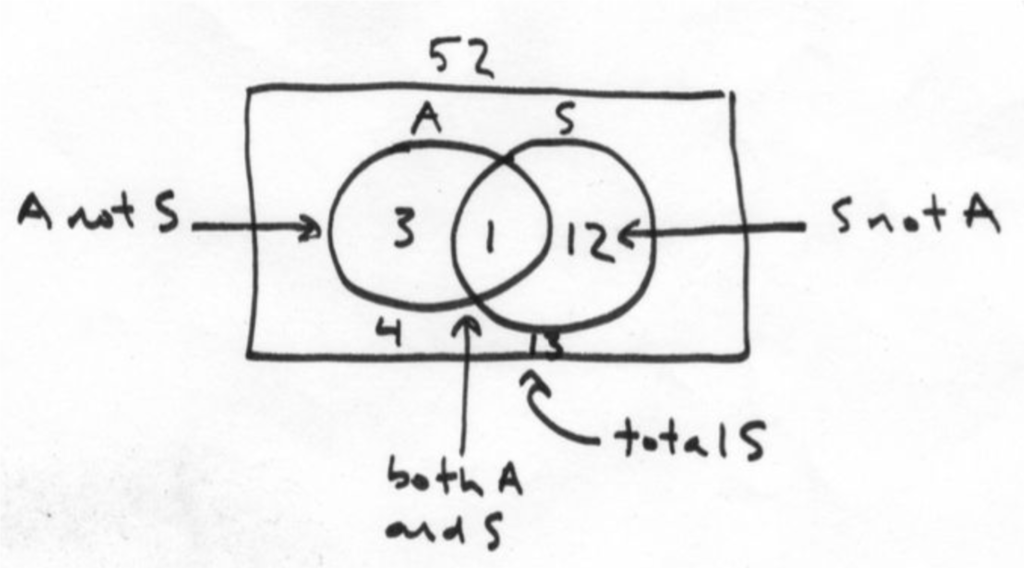
Now let’s put it back into the cards example:
1/13 + 1/4 – 1/52 = 16/52
And, of course, we can universalize that statement as follows:
P(A) + P(S) − P(A⋀S) = P(A⋁S)
That is, the Probability of pulling an Ace OR a Spade is the same as the Probability of pulling an Ace plus that of pulling a Spade, and then carefully remembering to take out the overlapping term by subtracting the Probability of Ace AND Spade.
That case where there’s no overlap
This is known as “mutually exclusive,” in case you’re interested, but that terminology is useless for GMAT purposes so let’s just shitcan it right now.
Then again, if it’s one of those terms that you’ve used without ever really putting thought into what it, you know, actually means… you’re welcome.
Question: what happens to the OR case if there’s no center term that’s shared?
Well, it’s as straightforward as to say that it’s the Probability of Thing A Happening plus the Probability of Thing B Happening.
Like this:
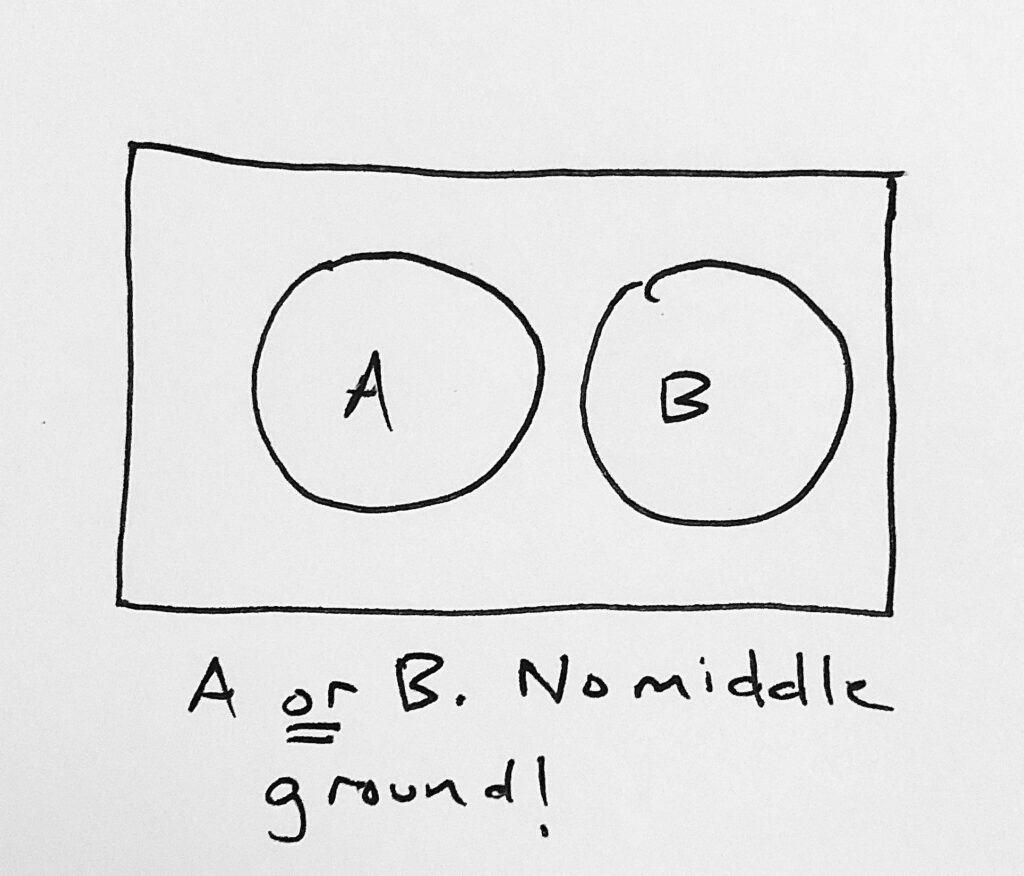
Notice how there’s no overlap? It isn’t going to work with our current card example, because, obviously, the Ace of Spades is both Ace and Spade.
The place where this applies is where no card shares the two qualities as defined by each circle: that is, something such as the Probability that we pull a card that is either an Ace or a Jack.
Clearly none of the Aces are Jacks and vice-versa, so this is a case where we see no overlap.
How is the Math Different?
In point of fact, it’s not.
Your overlap term is still there, but it’s just zero; in other words, the Probability of Ace and Jack is zero:
P(AandJ) = 0
Our total Probability is thus written:
P(AorJ) = P(A) + P(J) − P(AandJ)
Particularly in Probability and Combinatorics, it can be useful to write out “ghost terms” such as
these because it will help you work out the logic of what you’re trying to say.
Frustratingly, a lot of textbooks will simply drop terms that are adding zero or multiplying by one because they don’t affect the answer. That’s all well and good, but it’s confusing as shit6 just to see those terms myseriously vanish and I’m fairly convinced that this is done just to make half the class feel stupid.
Look at it this way: whatever you’ve been taught in the past, I’m giving you permission to write a bit more here. The trade-off seems reasonably clear: if you write more things and get a question correct, that is better than writing fewer things and getting the question incorrect, yes?
Good. I thought so.
And now for a quick recap…
One of the best ways to analyze Probability is to think of whether you’re narrowing or broadening the field of your choices.
From the general sense of the question, that should be pretty easy to do. It’s a simple: do you reckon7 this will give you more fewer options (multiply) or more options (add)?
Want more information about GMAT Probability? Check out this article.
Are you really serious about improving your GMAT Probability skills? Check out my full GMAT Probability Guide at Podia.
The GMAT Probability GuideAny questions? Talk to GMAT Tutor Online Rowan Hand right there, above!





