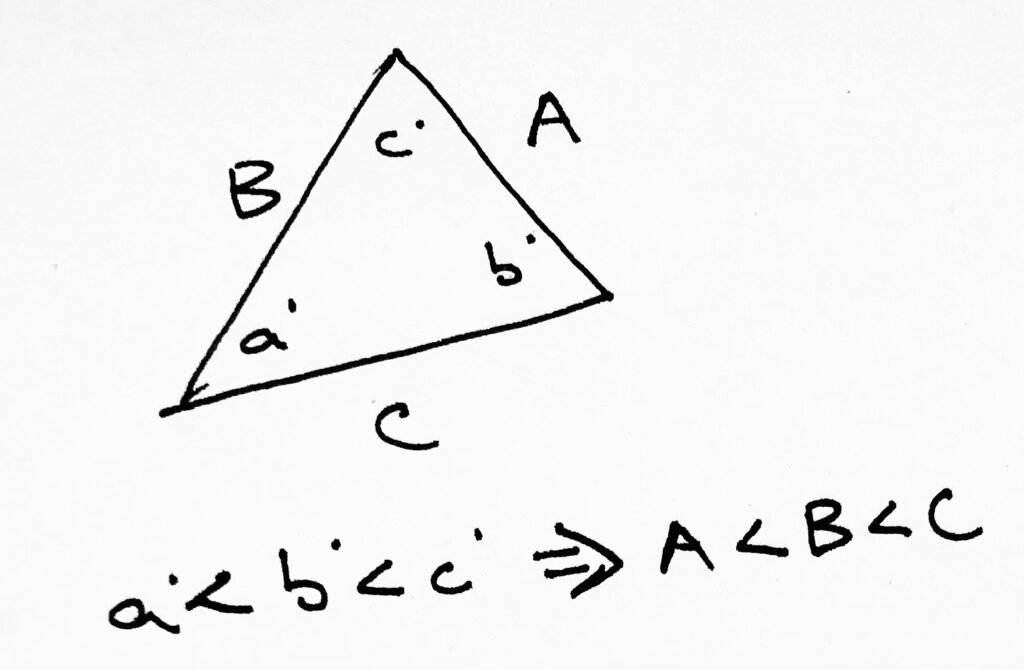
Ultimate Guide to GMAT Geometry, Part II: Polygons, Perimeter and Area, Parallelograms
Chapter 5: Polygons in GMAT Geometry
Remember how I’ve mentioned like ten times about how a straight line creates a 180-degree angle? If not, well, it does.
Now, think about this. What happens if we were to magically fracture that line? If we broke it in one place, we could imagine a new object that looks like this:
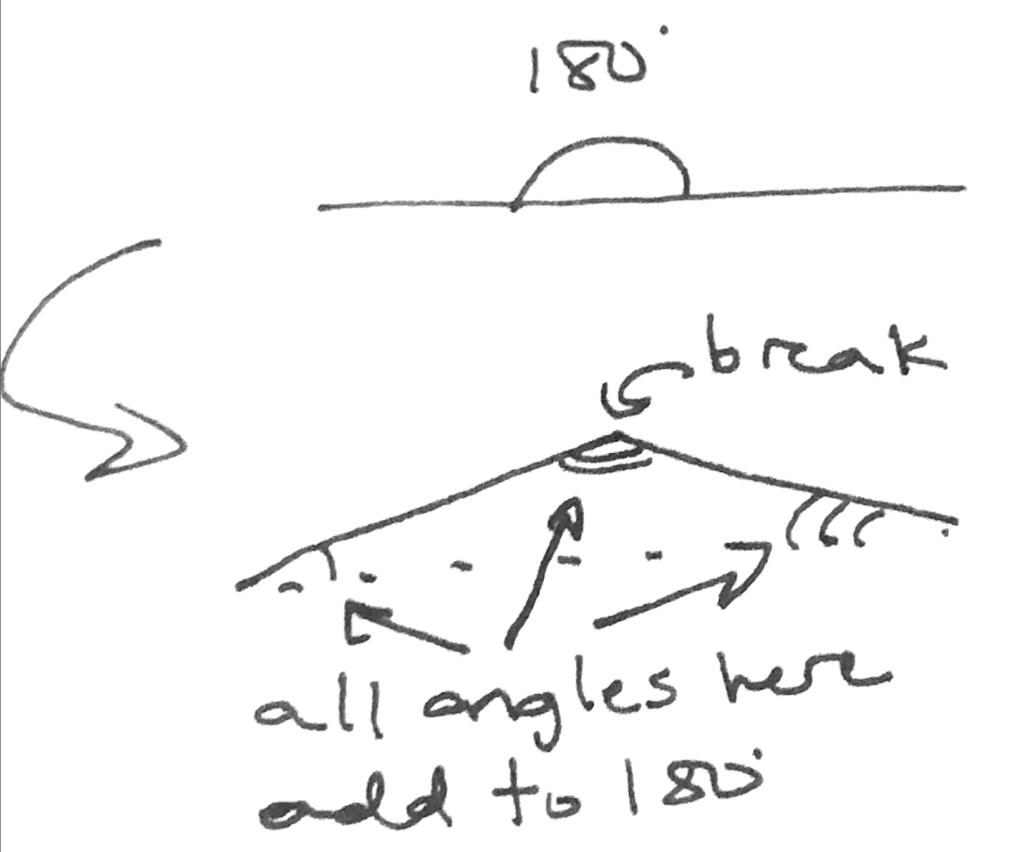
You might recognize this as what is commonly called a triangle, or a three-sided object. Yes, I really hope you knew that before I said it. You’ll note that those 180 degrees that were in the original line are now distributed among all the angles within the triangle.
In other words, the sum of angles in a triangle is 180 degrees.
Now imagine we were to do the same process again to one of the sides of the triangle:
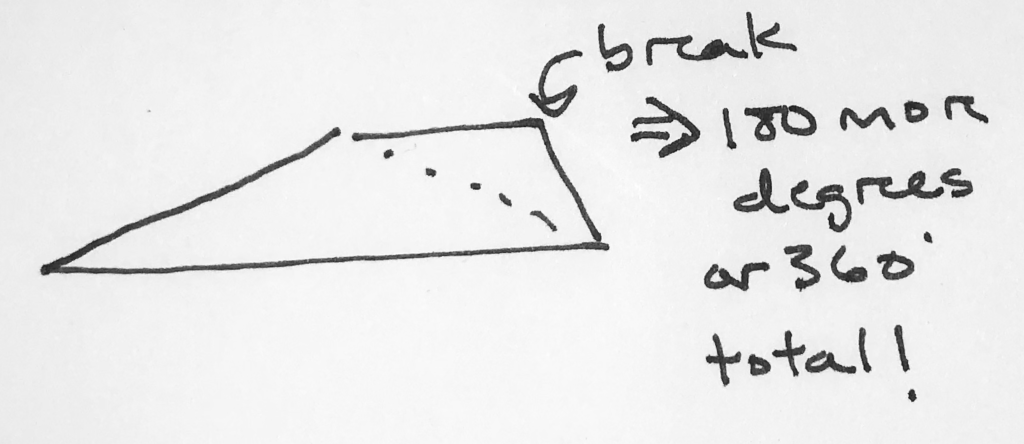
This creates a four-sided object, or a quadrilateral.
Now we see that the 180 degrees of that side of the triangle are distributed into the full object such that we now have the 180 original degrees of the triangle plus another 180 degrees.
In other words, the sum of angles in a quadrilateral is 360 degrees.
Now if we were to do it again, we’d get a five-sided object or a pentagon. We’d also add 180 degrees from the line we just snapped.
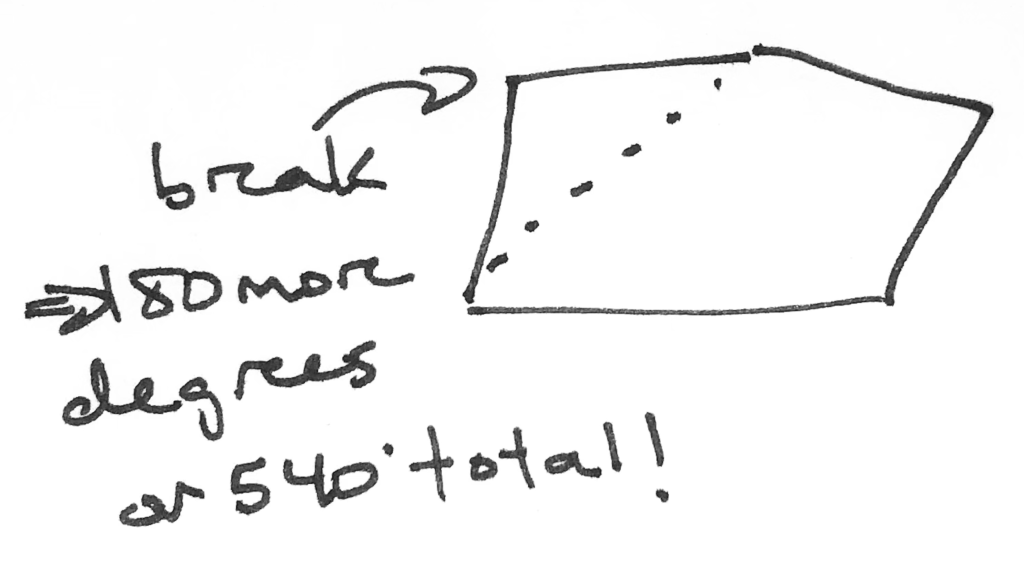
In other words the sum of angles in a quadrilateral is 360 + 180 = 540 degrees.
We could keep going here, but I’m going to assume that the process is fairly clear by now. All that we need to do is to put the pieces together and figure out how to calculate the sum of angles in an object based on its number of sides.
Let’s start with a triangle, because there’s no way to close an object (one made of straight lines, at least) without a minimum of three lines. If we call the number of sides n, we could say that the sum of the angles in the object is:

Go ahead and try this for four, five, six, and seven sides. You’ll be amazed to see the right numbers come out–I mean, that is, unless you did the arithmetic wrong, but you know what I mean.
See what I mean? Remember, the purpose of the formula is so that you don’t have to memorize the specific values, but it’s probably good if you have the values more or less in your back pocket for polygons of 3, 4, 5, and 6 sides.
Chapter 6: GMAT Geometry does Perimeter and Area
The perimeter of an object is described as the sum of the length of its sides. In other words, find a way to get the length of all the sides, add them up, and that’s your perimeter. This is measured in units of length, obviously, such as feet or meters.
The area of an object is much more abstract: it is described as the amount of space within an object. I mean hopefully you know this all already, but as I write it, it makes me realize that area is quite a strange little concept.
Area is most simply defined using two dimensions: length and width. Both of these would be in, say, feet. The area of an object would be its length times its width, giving a unit in, to continue with the same example, feet squared or ft^2.
We probably all sort of understand what area is supposed to represent, but when we try to think about it in the real world–WTF is area, really?–we see that it is largely useful in the world of real estate and not much more unless we get into really specific, granular examples such as calculating something’s surface area in a design or engineering context.
ASIDE: It might be worth noting here that if you have one measurement in feet and one in meters, for example, it would be useful to convert both to the same unit of length–preferably the unit seen in the answer choices, yes? That is, feet x meters does technically describe an area, but it’s also a pile of horseshit as far as the answers go. Keep your units straight and convert when necessary.
This works great for rectangles and squares, where the length and width are bloody obvious, but it becomes a bit of a pain in the ass for triangles or any other funny-shaped objects.
Perhaps what would make a better idea of area is to consider square tiles. Think about it like this: when you consider a one foot by one foot tile, how many of those tiles would fit within the object? That’s how many square feet are in the object.
Now this of course might seem only to apply to objects that can easily be described by square tiles. That’s not necessarily true, as long as we’re willing to abstract the concept of area into smaller and smaller terms. That is, for example, if you take half a tile, you get ½ feet squared or a quarter of a tile gives ¼ feet squared.
We’ll see more of that as we go along, but here’s one nice little imprecise rule of thumb for the road.
For an object of a given perimeter, the more equal all of your sides are, the greater the area of the object. Conversely, for an object of a given area, the more long and skinny the object, the greater the perimeter.
I’d hesitate to say that there’s a perfectly strict rule about the relationship between area and perimeter, but that one holds fairly well for our purposes here.
And, just as a reminder, always check a survey map if you’re going to buy a plot of land. If it’s one foot wide and a mile long, that will give you a whopping 5280 ft^2 area… that you can only stand sideways in.
Chapter 7: GMAT Geometry and Parallelograms
A parallelogram is any object with two sets of parallel sides. Like these:

Yes–you can probably see from this that the term “parallelogram” might be broader than one originally thought. It includes all rectangles and all squares, because, of course, rectangles and squares all have two sets of parallel sides.
Now, the perimeter of a parallelogram is easy: just add all the sides up. Even better, you can tell by virtue of the fact that both sets of opposite sides are parallel that the lengths of each opposite side must also be equal!
Now, don’t break your brain on this point because you’re unlikely to be asked about it, but it’s worth exploring this on your own to get a feel for it. Take a piece of paper and try really really hard to draw a parallelogram with unequal sides and you’ll get what I mean.
Even better, since the opposite sides are equal, we can calculate the perimeter as simply 2x+2y. Like this:

At this point, the fun stops like a dart in someone’s eye. The area of a parallelogram isn’t anywhere as easy as it sounds.
A good general rule for GMAT Geometry is that to determine the area of an object, we need the vertical height. In fact, the term “height,” for our purposes, must always mean vertical height (90 degrees from the base).
For a parallelogram, this presents itself as such:

You will notice, then that this describes the difference in the area between a rectangle and a parallelogram.
The rectcangle uses the actual side as its height, which is the maximum possible. Anything else will shrink because the side becomes the hypotenuse of the triangle here, while the vertical height is one of the legs:
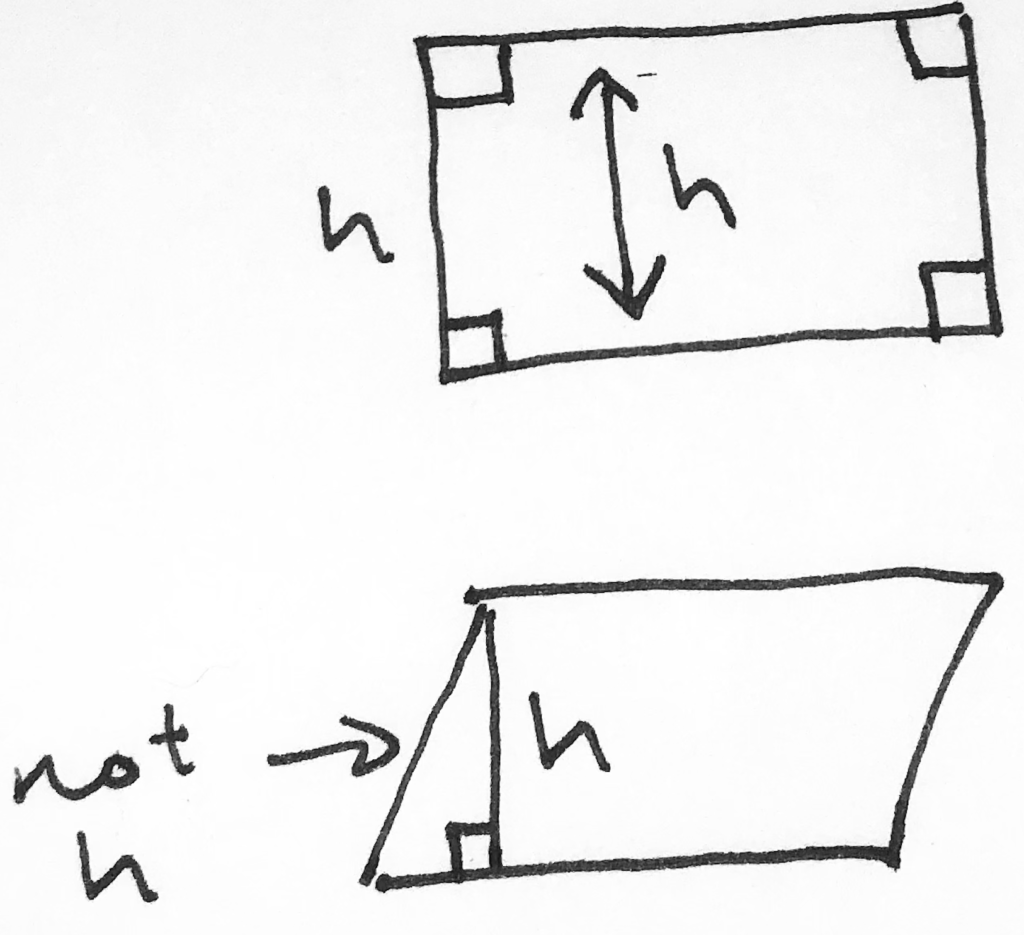
As we’ll address in a lot more detail later, the hypotenuse must always be longer than either of the legs. In short, by definition, the more that a parallelogram is tilted…
…the less area inside it. Just try with your hands and see!
One useful fact is that because the perimeter is 2x+2y, we know that the non-equal angles must correspond to the lengths xandy. If we say that the angle a is opposite side x and the angle bis opposite side y, then we can also say that 2a+2b=360. It follows that a+b=180.
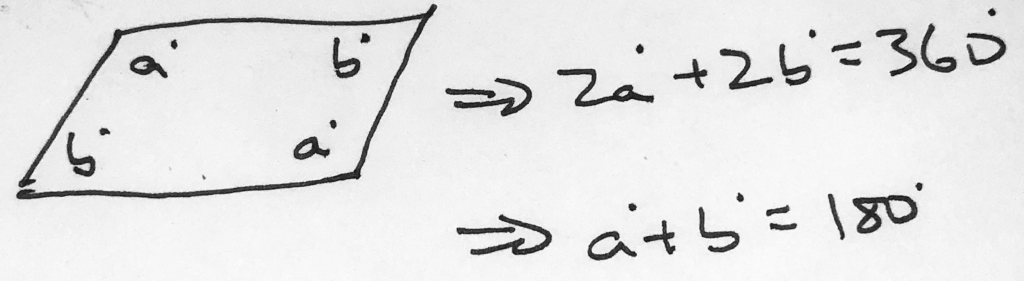
In short, what we can see from this little demonstration is that the two non-equal angles in a parallelogram must always add to 180 degrees. No reason to mess around with the full 360 just to arrive back at this point.
One non-useful fact, just to be complete, you do not need to know that an equilateral parallelogram is called a rhombus. If the question uses the word “rhombus” and doesn’t define it, then you’re looking at a non-Official GMAT question of questionable use in your study. Up to you, but I wouldn’t waste my time.