The Ultimate Guide to GMAT Geometry (Part I)
Geometry has a really weird relationship with the GMAT. It’s the one place where quite a bit of memorization is necessary, which causes a big problem: imperfect memorization will lead to wrong results.
For that reason, I think memorization of rote formulae is mostly a waste of time. After all, the GMAT has a nasty way of asking probing questions that test whether you truly understand what a formula means rather than expecting you to be able to blindly plug and chug the way you probably did all throughout high school.
With all this in mind, I’d suggest no more rote memorization than necessary for GMAT Quant. However, to succeed in Geometry–particularly with Trigonometry–a fair bit of memorization is inevitable.
One (very imprecise) way to think about this is that Arithmetic and Algebra are largely “derived.” That is, they are built up of a set of simple rules and stay within the bounds of those rules.
Geometry, on the other hand, is observed; that is, many things about Geometry are actually seen in nature, or at the very least can be imagined as idealized consequences of physical actions: for example, the suggestion that “a perfect circle” can be created by planting a stick in the ground, tying a rope to it, and walking a circumference that keeps the rope perfectly taut. We’ll see this sort of idealization with regard to a lot of definitions.
Of course this type of thinking about Geometry risks confusing the world of Platonic Ideal with the world of matter, which is probably a mistake in a deeper, philosophical sense. Furthermore, it isn’t as if geometry is without its own axioms and postulates, cf. the Pythagorean Theorem.
Luckily, the GMAT has no time for all that navel-gazing horseshit. That leaves us free to talk about the things that work on this exam.
Let’s get into it.
Let’s build up Geometry from the simplest object I can think of: a straight line.
GMAT Geometry with Lines and Line Segments — Chapter 1
Well, this is embarrassing. I’d hope that you would at least know what a “line” is or maybe the GMAT isn’t for you.
Putting that aside, I’ll say that a line is a continuous measure of length, infinitely thin. In other words, it just traces movement along a certain direction, but with no area.
For example, the line containing Point A and Point B would be described as such:
That said, a “line,” per se, is infinite. It goes on forever and ever.
Now, if we wanted to definite the endpoints of the line, we would describe it as a line segment. Like this:
In other words, a line is infinite, while a line segment is finite. That is, no little arrows pointing off the end, because anything with little arrows pointing off the end is, naturally, infinite.
The last thing we need to realize here–as in, the term might appear on the GMAT–is that points that exist on the same line are referred to as collinear.
In this case, the points A, B, and C are collinear.
GMAT Geometry and Angles — Chapter 2
Now when we put more than one line near each other, shit gets real.
If two lines aren’t parallel, they will, eventually, intersect one another. Seriously! Think about this: if there’s any pitch at all to either line, at some point in the distance they will actually intersect.
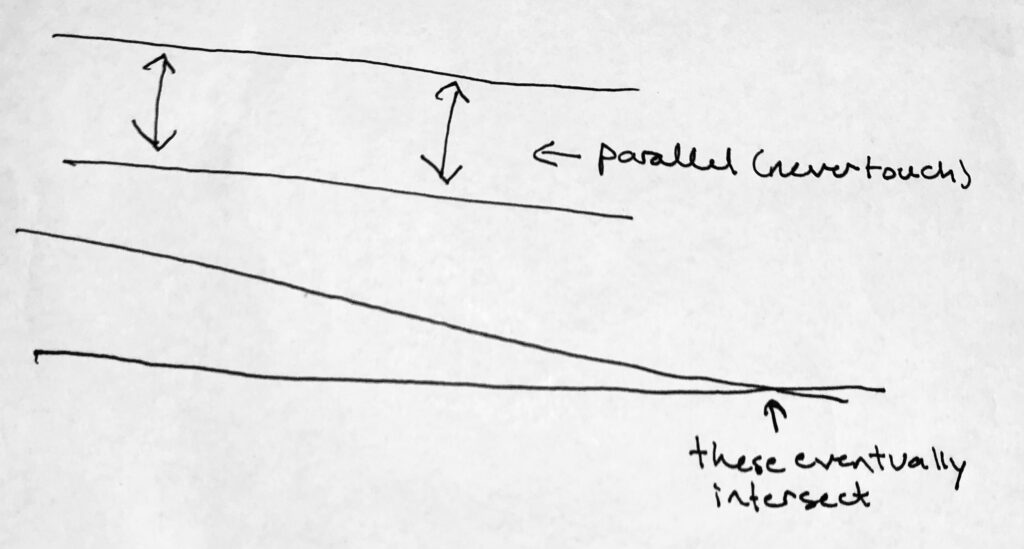
If you can imagine extending those lines out infinitely far, you’ll realize that it simply doesn’t matter: if the lines aren’t exactly parallel to one another they must meet!
Now, the pitch at which those angles meet is traditionally called an “angle.” An angle is measured in what’s called “degrees.” I’m going to play fast-and-loose with the “degree” sign here because I can’t be bothered to draw a little dot on every stupid angle I draw, so deal with it.
That’s hopefully obvious–we aren’t six years old–so let’s not belabor the point.
That said, here’s where we start getting into definitions that begin to matter and will require a bit of memorization. The good news is that you probably know most of this already. The bad news is that if you don’t, you’d better fucking learn it, yes?
First, there are only ever 360 degrees. No matter how much you travel round and round on a flat plane (like a piece of paper), you can only go from 0 to 360 degrees. Like this:
I mean I guess that’s the point if you’re going from one point back to the point you started from. There are minor exceptions if you start breaking up the lines, but let’s talk about that when we get there.
Now, given that going back to the point we started at implies 360 degrees, we can infer that going exactly halfway implies 180 degrees. Like this:
It might be obvious at this point that when you exactly halfway from where you started, you have formed a straight line. Well, then, it seems that a straight line can also imply a 180-degree angle. Like this:
Even more revolutionary, if you go one-fourth of the way–half a straight line–and simply make a 90-degree angle, you’ll get, well, a 90-degree angle.
Now some books would have you know that two angles that add to be 90 degrees are “complementary,” while two angle that add to 180 degrees are “supplementary.” The question for me is why you’d waste precious, limited brainspace on such nonsense if it won’t appear directly on GMAT Geometry.
And… yes, that’s all there is to it. Aren’t you glad you asked?
Chapter 3: Acute vs. Obtuse Angles
Yet again, I don’t mean to insult anyone’s intelligence here, since most people do and probably should know what “acute” vs. “obtuse” means in the Geometry sense. That is, not “non-chronic” and “intentionally difficult,” respectively, although I suppose they could be such things if you really wanted…
Simply, an acute angle is an angle that is less than 90 degrees. When you draw it, the lines themselves look all sharp and pointy. Like this:
An obtuse angle, on the other hand, is an angle that is greater than 90 degrees. This one is a bit more difficult to describe. I suppose we could say that the lines make a “softer” shape, but let’s keep poetry out of this.
Perhaps a better way to phrase it would be that the space between the lines, the “negative space,” actually makes something sharp and pointy. Like this:
Now, one interesting thing about this is that we have discussed “greater than 90 degrees” and “less than 90 degrees,” but you’ll notice we never said “exactly 90 degrees.” There’s a reason for this: a 90-degree angle is called a “right angle.”
You could also call it a 90-degree angle, of course, but that would be taking all the fun out of our little naming adventure, now wouldn’t it?
There are loads of things you can do with right angles, particularly when we get into triangles, but let’s leave that for later.
GMAT Geometry and Parallel Lines (or: Where Blondie Got That Album Title) — Chapter 4
This one probably starts off most simply with a definition that we’ve already sort of touched on: “parallel lines” are two lines that never touch each other at any point in space.
The practical implication of this, of course, means that these lines have precisely the same slope (pitch, or their angle relative to the horizontal), but are at different places in space.
If they had the same pitch and were at the same place, they would be, well, the same line.
(This “slope” business will come up in more detail in the Coordinate Geometry sector, so just relax.)
Remember that the only reason the lines don’t touch is because they maintain this exact-same pitch no matter how far out we take them.
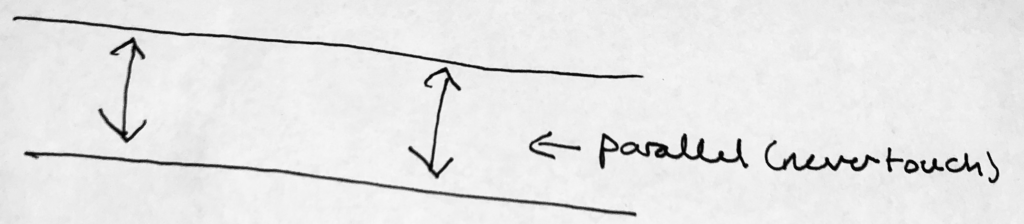
Now there exist all kinds of fun things that we can do with parallel lines, most notably that if we take a third line that crosses both (and any line that isn’t parallel to the other two would do so…), we can see the relationship between all of the angles on both parallel lines. Crazy.
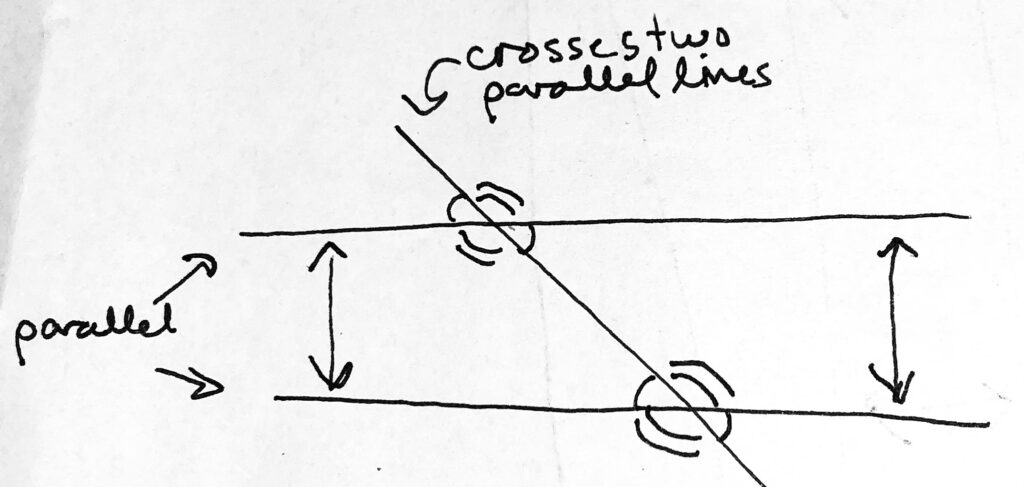
Remember that a line itself can be considered a 180-degree angle. Then, if we’re given even one of the angles created as our third line intersects one of the parallel lines, we can tell the values of all the angles on both parallel lines. Like this:
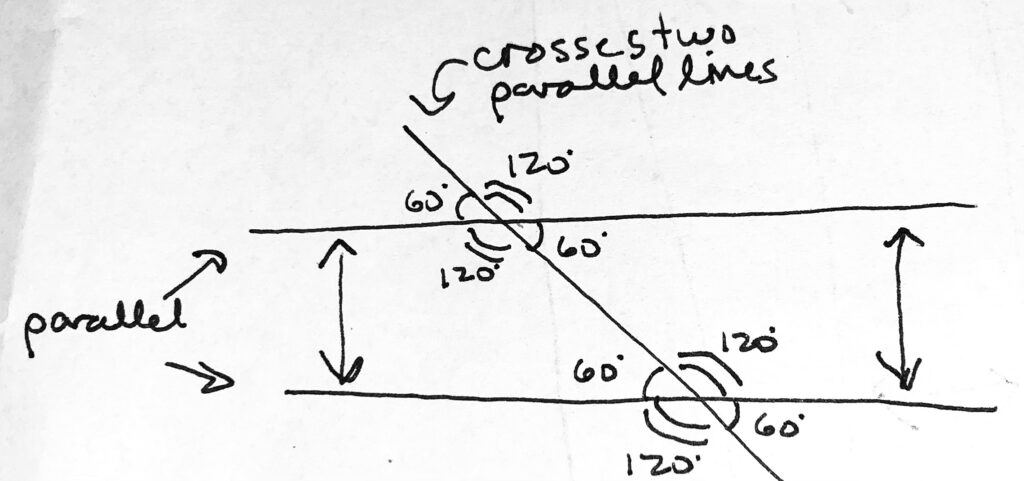
That’s a lot of information to get out of a simple rule. Nice.





