How do you know that a GMAT Quant question is tricking you?
Read on…
Of course the GMAT is trying to trick you. That’s the whole point. You probably thought you’d learn some “tricks” and be able to get a 700+. Excuse my giggling.
No, that’s just GMAT Quant tricking you, I’m afraid. Like an evil pimp.
Don’t let it succeed.
The question we have here is a classic GMAT Quant trick.
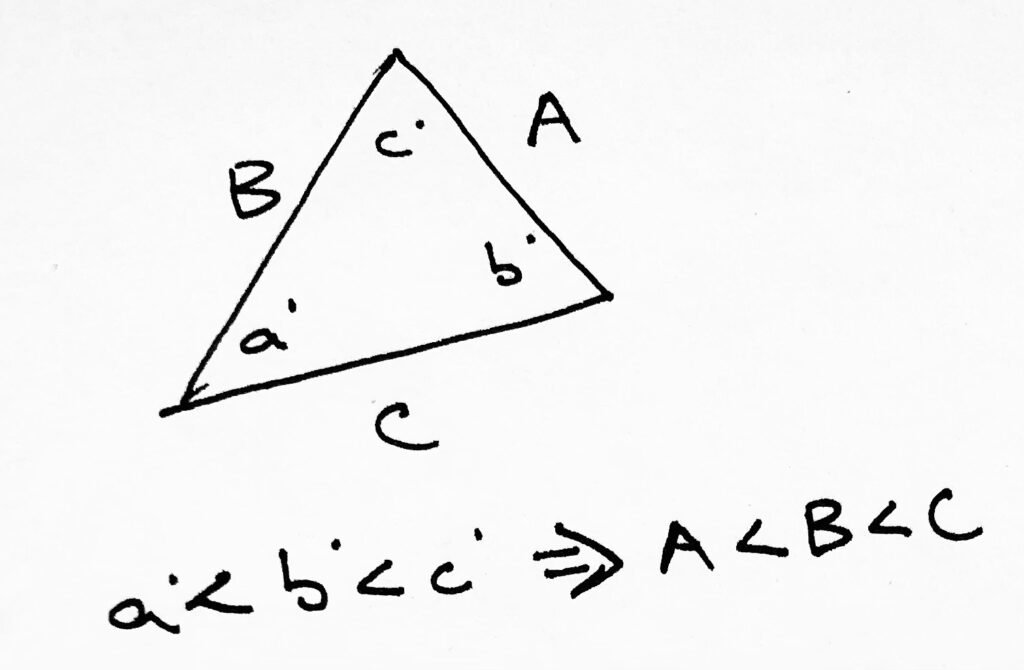
Check this: they give you something obvious (a 45-45-90 triangle), but then they twist it so that it doesn’t work properly. That damned sqrt2 isn’t on the hypotenuse! Egads!
Actually, the correct answer is only one small adjustment away, but if you can’t identify the little change to make you’ll be in huge trouble! It’s very easy to feel overwhelmed by questions such as this one and end up thinking maybe you have the wrong triangle or something… but it’s an Isosceles Right! That is a 45-45-90!
No, there’s something not totally obvious going on here. It’s more of a problem of confidence for most people–learning to be a bit cocky with these questions allows you to plow forward. Being slightly arrogant about your math ability might get you into hot water from time to time, but let me assure you that it will provide many more answers than thinking you are unable to answer…
GMAT QUANT is ALWAYS TRYING TO MESS WITH YOU. It’s time to figure out how. Eventually, as in this question, you’ll learn to see “the point of the problem” and then you’ll know where to stop.
In this case, I can see that 16sqrt2 will never be the hypotenuse because the other two sides don’t add up properly. That opens me up to test the other answer choices as possibilities.
However, notice that the other number actually mentioned in the question is 16–why not start there? Lo and behold, when you calculate with 16 you get the answer. That saved you the hassle of going through the answers one-by-one.
Simple.
The perimeter of a certain isosceles right triangle is 16+16sqrt(2). What is the length of the hypotenuse of the triangle?

He knows the answer.