The Ultimate Guide to GMAT Geometry, Part III: Trapezoids, Rectangles, and Squares
Chapter 8: Trapezoids (Trapeziums (Trapeziae?)) in GMAT Geometry
If you were paying attention to the footnotes, then you’d recognize this as the extra credit answer.
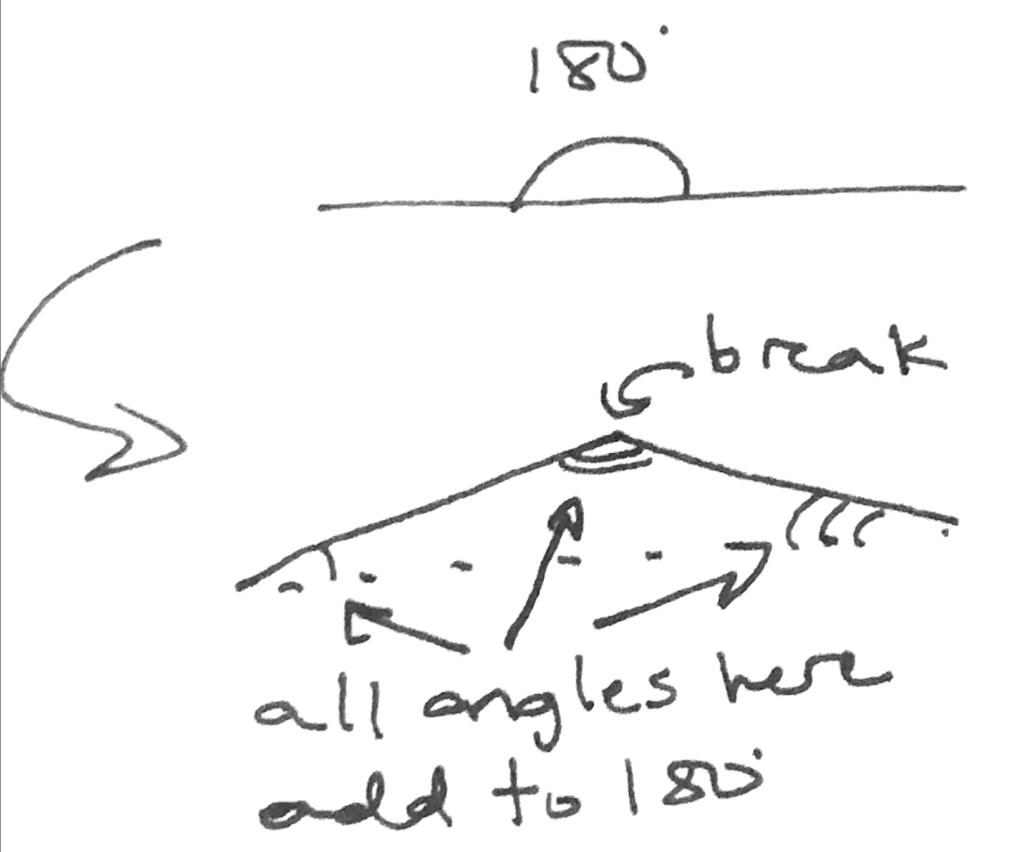
In essence, a trapezoid is sort of a dodgy parallelogram, where only two of the opposite sides got parallel. The problem here is that there’s now no reason for any of the sides to be equal. Draw it and see!
Now I’ll spare you the “trapeze” joke but there is a funny thing about the name of this object…
If you’re from anywhere but North America you’ve probably learned the object as “trapezium,” but it’s exactly the same thing. It’s just that the “oid” suffix is what GMAT Geometry uses, plus it is superior because it just sounds more like something out of science fiction. That is, you don’t hire Harrison Ford to kill your miscreant andriums when they get loose. Just saying.
Nice thing: the perimeter is still quite straightforward–just add up all the sides and see what happens.
Now as far as the area goes, we actually do have a way to do it that’s not shabby at all. Provided that we know the height of the trapezoid–and we really do need to know the height!–then we simply average the two bases and multiply by the height.
In other words, instead of base x height as for a normal rectangle or parallelogram, we get the average of the two bases x height. Like this:
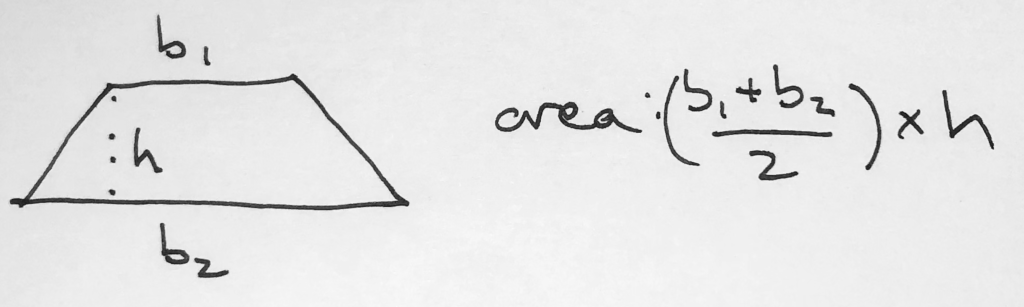
Just note that the height will have to be provided one way or another. Either it’s vertical or it is easily inferable. If neither, we simply aren’t going to be able to get the area–no way to get the height? That’s your E answer in a DS question.
As a final note, the bases here simply need to be your parallel sides. They don’t necessarily have to be horizontal. That is, the orientation of the object makes no difference when using our area formula. Check it out:
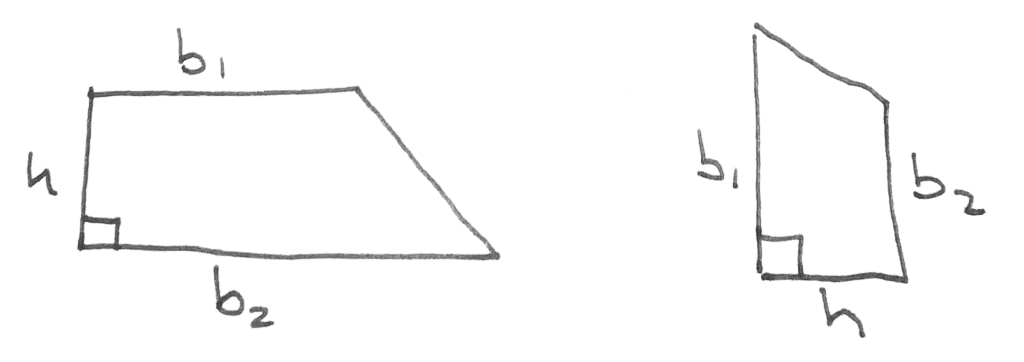
See, that wasn’t so hard after all.
Chapter 9: Rectangles
This is a bit of a breath of fresh air. There are only a couple of things to note about rectangles that aren’t completely obvious.
First, the rectangle is, of course, a parallelogram, but it also has four right angles. Now, in fact, we can use this point to cut down the definition simply to that: any four-sided object with four right angles must in fact be a rectangle–try to draw one that isn’t!
Therefore, we can say that a rectangle is any four-sided object with four right angles.
As with any parallelogram with non-equal sides x and y, we can say that the perimeter of a rectangle is 2x+2y.
The area of a rectangle is, then, of course, xy. Do we need to discuss this any further?
Chapter 10: Squares in GMAT Geometry
It’s chapter 10 and ten is a nice round number, but if I were really clever, I would have made it Chapter 9 because 9 is a perfect square. Oh, well.
ANYWAY… the thing with squares is that squares are just well-behaved rectangles: not only do they have four right angles, they also have–wait for it–four equal sides.
“A square is actually a rectangle?” you might gasp, but I assure you that it is true. All squares are rectangles: we just established that all squares have four right angles, yes?
Now, the converse of this statement is not true: while all squares are rectangles, it is not of course true that all rectangles are squares. Clearly there exist rectangles that do not have four equal sides. Put another way, this would be a bit like saying that just because Americans tend to talk louder than other people that all people who talk loud are American. I’ll leave the proof of that one up to your surely fertile imaginations.
The perimeter of a square gets really easy. Since we don’t have different side lengths, we can say that for a side length of x, we know that the perimeter is simply 4x.
Likewise, the area is extremely easy. Chew on this for a moment: since the length and the width are both x, we don’t need to write xx. We can simply write x2. You know, “x squared.” Curiously convenient, wouldn’t you say?
Now, that said, one other thing that’s going to come back to us later as we discuss 45:45:90 triangles is the diagonal of a square.
One thing that you can take to the bank is that because squares are consistent objects that always have the same proportion, you can remember that for a square of side x, the diagonal must be x2. You don’t need to memorize that just yet; just stay tuned for more on this one.